ЗАДАНИЕ 3
№ 1. Найдите все трехзначные числа, равные сумме кубов своих
цифр. (6 баллов)
Например, число 123 не равно 36 = 13+23+33,
а вот 153 = 13+53+33.
№ 2. В саду M*M деревьев посажены квадратом со стороной M-1.
Т.е. в M рядов, по M деревьев в каждом (расстояния между
деревьями в ряду и между рядами равны 1).
Найти количество K деревьев, расположенных внутри кольца
(деревья, расположенные на границе кольца не считаются)
с внешним радиусом Ro, внутренним радиусом Ri и центром,
совпадающим с центром квадрата.
Учтите, что
а) Ro и Ri не обязательно целые,
б) а M может быть и четным. (12 баллов)
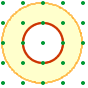Входные данные: M, Ro, Ri.
Выходные данные: K.
Например, если M=5, Ro=2 и Ri=1, то K=4 (см. рисунок)
№ 3. Даны две строки A и B, каждая из которых является
предложением, которое оканчивается точкой. В этих
предложениях слова отделены друга одним пробелом.
Известно, что все слова в пределах каждого предложения
различны.
Выяснить, можно ли из слов предложения A получить
предложение B. (8 баллов)
Например, из слов предложения
A='Из всех искусств важнейшим для нас
является Искусство Программирования.'
можно составить B='Искусство для всех нас.'
Входные данные: A, B.
Выходные данные: Сообщение: "МОЖНО" или "НЕЛЬЗЯ".
Назад 